Parallel Unique Path (PUP) Carving, Illustrated
What is PUP carving?
Parallel Unique Path (PUP) carving is one of the advanced file carving methods.
It is used to reconstruct fragmented files without any use of filesystem metadata by finding and assembling file fragments.
Some other methods are described there.
PUP carving requires two things:
- An ability to identify file start (file header),
-
a proximity function (also called weight function) which tells us how good is the match between two clusters.
It tells us how likely any given cluster is the next cluster for the given incomplete cluster chain.
It is also nice to be able to identify the end of the file,
either by detecting the file footer or knowing the file size.
This is optional, though.
Simple example
Let's see how this works.
Typically, the proximity function provides a number, either a percentage or using some other scale.
For illustration purposes, I will show proximity function output as line thickness – a double line means a strong signal,
a single solid line means an average signal, and a dashed line is for a weak signal.
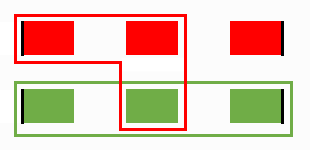
We have six clusters in two files – red and green.
File headers are on the left, and footers are on the right.
The initial step is to identify and mark headers.
Step 0 start

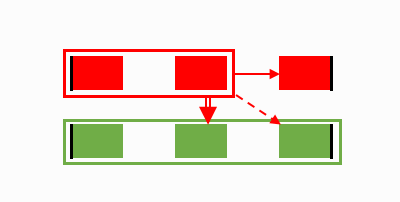
Then, compute proximity function values from headers to all unassigned clusters. This requires eight computations.
Step 0 proximity functions
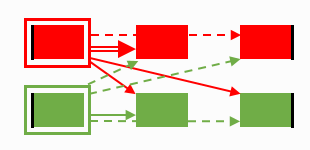
Once this is done, we select the strongest available signal and associate the appropriate cluster (red middle) with its incomplete file (red).
That is, we choose the file for which the next cluster is best defined
and advance the process one step by attaching that cluster to its corresponding file.
It is important that we only do it one step at a time.
The result is as follows:
Step 1 start
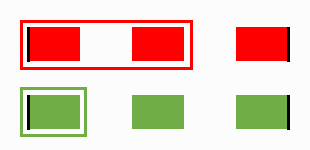
The process is repeated, but clusters already assigned to their respective files are
not considered candidates for analysis.
This accounts for the Unique in the Parallel Unique Path algorithm,
which is the important point, as we will discover shortly.
For now, let's watch the process to the end.
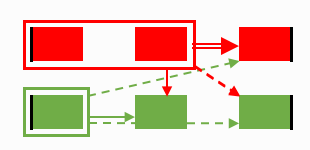
Step 2
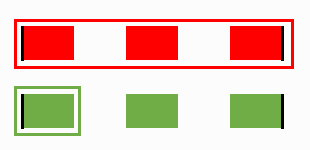
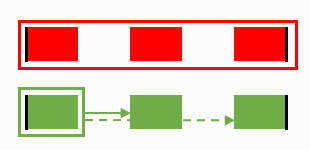
Step 3
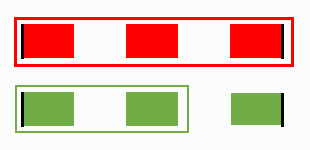
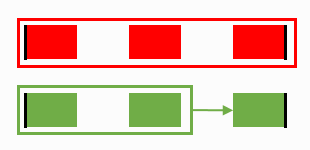
Final result
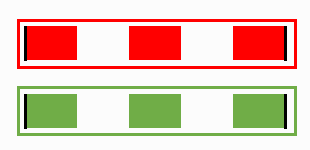
Finally, we have two files properly reconstructed.
You may notice that fewer and fewer proximity functions are needed further into the analysis.
The computation effort required per step decreases with each step.
More complex example
In real life, we will be dealing with tens or hundreds of files and millions of clusters,
and it is overly optimistic to assume
the proximity function output is correct in all cases.
That does not happen.
Let's see what happens if an error occurs in one of the iterations.
I will stick to the same example for the sake of simplicity.
In this example, the red file produces a strong wrong signal and the wrong cluster is added.
Proximity calculation gone wrong...
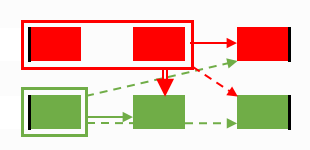
... and its results
If we comply with the unique path requirement, nothing is recoverable.
The recovery of the red file went wrong, and it now blocks the green file from claiming its middle-green cluster.
No matter how the proximities play out further, the green file is not getting reconstructed.
So, incorrect recovery of one file leads to incorrect recovery of some other file.
This thing is called error propagation or cascading errors.
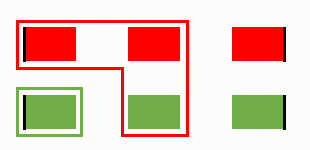
It may seem quite an obvious solution to stop requiring paths to be unique.
If two files are allowed to take the same cluster, the problem seems to go away,
allowing at least one file to be recovered,
as in this example:
Non-unique paths, the first step...
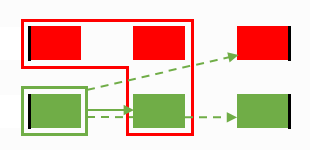
...the first step result and the updated proximity map...
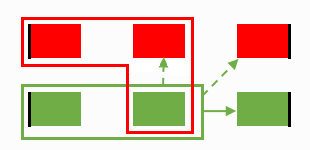
...and the final result.
It seems like not requiring paths to be unique does help... or does it?
First, if clusters can be reused, the number of calculations increases.
Following the correct recovery flow (the first example),
you can see that the number of proximity function calculations at each step decreases
from the initial eight to just one in the last step.
Losing that, however, is not that bad in practice.
Much more important is that unique path requirement also works another way round, in some cases improving the result.
See, there are two sides to the unique part requirement.
At some point, the proximity function erroneously assigns a higher score to the incorrect cluster A
instead of the correct cluster B.
As often happens in practice, A comes out as the best result and B as the second best.
Then, one of the two things occurs:
-
If the error occurs when cluster A is not assigned to a file yet, it is assigned to the wrong file.
This later causes error propagation.
-
Suppose the error occurs when cluster A is already assigned to a file.
The algorithm is forced to take cluster B instead, thus recovering from a proximity function error, as illustrated below.
Recovering from proximity function errors
Practically, enforcing paths to be unique does more good than harm.
As each iteration uses the best available signal, the strongest signals are generally acted on first,
and weaker signals are used last when the choice of the cluster to pick is significantly limited.
Strong signals are generally more trustworthy, and by the time we need to use a less trustworthy weak signal,
the choice and the number of ways for a weak signal to screw up the process is significantly limited.
So, this is how the PUP algorithm works and why the paths better be unique.
References and what else you can read on this topic
- Rainer Poisel, Simon Tjoa, and Paul Tavolato. "Advanced File Carving Approaches for Multimedia Files." // Journal of Wireless Mobile Networks, Ubiquitous Computing, and Dependable Applications, volume: 2, number: 4, pp. 42-58.
- A. Pal and N. D. Memon, "The evolution of file carving," // IEEE Signal Processing Magazine, vol. 26, no. 2, pp. 59–71, March 2009.
Filed under: File carving.
Created Sunday, February 4, 2018