Navigation

File carving methods in data recovery

File carving is a process of searching for files in a data stream based on knowledge of file formats rather than any other metadata. Carving is useful when filesystem metadata is damaged or otherwise unusable. The FAT filesystem, typically used on small media, is the most common example. Once the file is deleted, or the media is formatted, the location data is lost because a filesystem zeroes out pointers to file contents.

Contiguous and fragmented files

A filesystem can store files on the media either in one chunk (contiguous, or non-fragmented files) or in several non-adjacent chunks (non-contiguous, or fragmented files).

Fragmentation occurs when there is not enough contiguous free space to write a file; the filesystem then has to split a file into parts that fit the available chunks of free space. Fragmentation also occurs when several files are written to the volume simultaneously and in other cases.

Fragmentation increases as the filesystem ages, as files are created and deleted. Larger files fragment more; this applies to higher-resolution still images and, to an even greater extent, to videos. It is common to have half or more of the video files on a memory card fragmented.

Carving for contiguous files

Any carving algorithm requires the ability to identify the file header. The first step in carving is to scan the media and produce the list of headers, which represent file start points. Once start points are located, there are several options to choose from

Header and fixed size carving. Take some fixed amount of data starting at the header. This method works for files where trailing data after the end of the file is ignored, which is true for most file formats. For example, given that JPEGs hardly exceed 100 MB (as of Q4 2022), one can capture 256 MB of data starting at the header. This naive approach will capture all contiguous JPEG files (although with excess data at the end of each file). The size limit can be adjusted for the specific task, file type, and camera settings. This method does not work with file formats that do not tolerate extra data after the end of the file, like the original Canon CRW.
Header and size carving. This method is a variation of the fixed size method, where we use the size derived from the header of the file instead of a fixed size. This only works for file formats where the file size is stored in the header. Files produced by this method do not have extra data at the end of the recovered file.
Header and footer carving. If a file has some identifiable footer at the end, the capture size can be limited to the nearest footer after the header, producing files with no excess data at the end. However, this method requires further adaptation to file formats that can be nested, the most notable example being JPEG with another JPEG thumbnail inside. With contiguous files, this situation is fortunately easy to detect, as detected points go in groups of four, two headers followed by two footers.

All these methods are fast. Processing speeds are limited mainly by the source media read speed.

Carving for fragmented files

Fragmented files are much more challenging to carve. We still have headers, and with luck, file sizes we extracted from these headers, but files are split into two or more fragments that are not necessarily in the correct order. To tackle this task, one needs a validation function and a similarity (proximity) function.

Validation and proximity functions

A validation function determines if the given file is correct or not. Good validation functions are exceedingly difficult to implement. Each file format requires its own validation function; furthermore, variations of the format require appropriate adjustments. If the file format is documented poorly or not at all, constructing a good validation function may be impossible. Validation functions are easiest to construct for file formats with their own checksums (ZIP or PNG). Loosely defined formats, like plain text or XML, are the worst.

A proximity function determines how likely it is that two blocks are, in fact, two adjacent blocks belonging to the same file, with the result expressed either as a probability or as some score measured in arbitrary units.

Bifragment gap carving

Bifragment gap carving is a method used to recover files in two sequential fragments with some extra data (gap) between them. The method's applicability is limited, but it has one significant advantage of not requiring a proximity function. You can implement bifragment gap carving based on the validation function alone. Let's see the diagram. We have a file header. Optionally, we can have a footer and the file size computed from the header. The distance between the header and the footer is D, and the file size from the header is S.

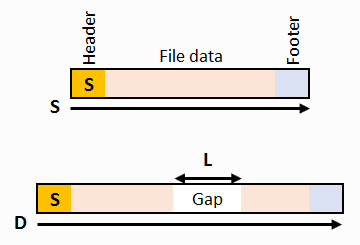
If there is no footer, the distance D is assumed to be some reasonable constant, large enough to accommodate both the largest possible gap and the largest possible file (assume D = L_max + S_max). The gap size L can be computed simply as L = D-S if S is known. Then, we need to do approximately N ~ (D-L)/B validation tests (for each possible position of a gap) and see which one produces the valid file. B here is a block size, typically 512 bytes.

There may be several positive validations if a validation function is not quite good. If this happens, several probable files are produced for the user to select the one needed. The first and last positions for the gap are not tested, because these outermost positions are known to be occupied by the header and the footer that are obviously parts of the file.

Then, if S is not known, we cannot determine the gap size, and we have to repeat the test for each possible gap size up to L_max = D-S_min, where S_min is some minimum acceptable file size. S_min is typically guessed by looking at known-good files produced by the same camera at the same settings. This makes for approximately N ~ ((D-L_max)/B)*(L_max/B) tests.

The inability to identify the footer does not change much, except that we must perform even more tests after assuming some maximum size D_max.

In the real world, ten validations can be performed per second per CPU core on a typical 20 MP image. Let's assume 50 validations per second with a mulicore system. Let's assume file size to be 10 MB, which is a bit on the small side but still reasonable. Typical sector size is 512 bytes. Sometimes, we can sniff the file system block size from what's left of the filesystem and use it. This improves speed, as we will soon see.

The time required to process a single header is, given a block size of 512 bytes (that is, with no filesystem cluster information)

Parameter	block size B = 512 bytes
D	10 MB + 32 KB	10 MB + 32 KB	D_max = 16 MB
S	10 MB	unknown	unknown
L	L = D - S	L_max = 256 KB	L_max = 256 KB
N	(D-L)/B	(L_max/B)(D-L_max*)/B	(L_max/B)(D_max-L_max*)/B
N	~20,000	~10,000,000	~16,000,000
Time	~ 6 min	~40 hrs	~70 hrs

and with a block size of 32 KB, as it would be if the filesystem cluster size is detected,

Parameter	block size B = 32 KB
D	10 MB + 32 KB	10 MB + 32 KB	D_max = 16 MB
S	10 MB	unknown	unknown
L	L = D - S	L_max = 256 KB	L_max = 256 KB
N	(D-L)/B	(L_max/B)(D-L_max*)/B	(L_max/B)(D_max-L_max*)/B
N	~320	~2500	~4000
Time	~ 6 sec	~50 sec	~80 sec

So, the time required increases drastically if not all parameters are known. If block size can be determined by some or other method, the scan time is inversely proportional to the number of sectors per block squared, which is fairly impressive.

The only drawback of bifragment gap carving is its limited applicability.

If you are interested, I have some real-life data on the applicability of bifragment gap carving here.

Complex fragmented file carving

There is no known single best algorithm to recover files from multiple fragments. There are various approaches and methods, but none are simple or fast. The simplest method is to apply the proximity function to all possible combinations of blocks and then merge blocks starting with the most proximate. This produces chains of blocks that most likely belong to their respective files, one chain corresponding to one file. One variant of implementing this is a Parallel Unique Path (PUP) carving algorithm. Unfortunately, the required amount of computation is proportional to a square of the number of blocks on the media, which is really slow.

Complex carving requires a proximity function. The proximity function is specific to the file format. If this is the image file, like JPEG, a variety of methods can be applied, starting with the simple color difference between adjacent points (first derivative), second derivative, or something fancier like Haar features, and then up to neural nets. One is not limited to just one proximity function; one can use any mix or combination.

There is a fine balance between the precision of the proximity function and its performance. Obviously, more complicated functions are slower. What's less obvious, more complicated functions tend to have some bias creep in, so they work well with one group of images and not quite as well with another group. For example, edge detection works well against a natural landscape photo while having problems with black-and-white text scans. So, it has to be augmented with a scene type detector for an acceptable result.

Various tricks are applied to reduce the amount of computation required. Blocks assigned to known-good files are excluded from the analysis. All-zero blocks or blocks that do not resemble parts of JPEG images can also be excluded. In real life, a set of heuristics is used for block identification to determine which blocks are skipped as candidates.

What Klennet Carver uses

Klennet Carver uses a combination of header-fixed size and complex carving using a mix of various proximity functions chosen to match to the specific situation. This provides a good balance between performance, as in not having to wait years for the scan to complete, and recovery effectiveness, that is, being able to actually recover fragmented files. Also, Klennet Carver uses a limited amount of bifragment carving during image recovery.